Bounding Box Orientation on Arbitrary Point Clouds with PCA

Last updated Oct 17, 2024 Edit Source

• Houdini
• Math

The most straight forward utility tool you can build using PCA is an automatic bbox generator. Even though the bound SOP can do the exact same thing, it’s still a nice exercise that helps you wrap your head around what principal components are and how you can use them.

I recommend reading the article on Principal Component Analysis first!

This works because the first PCA component gives you the direction, where the most variance occurs in your data. You could think of this as the longest distance through your point cloud. The components are ordered by importance and a perpendicular to each other. So the second one is the direction that has the second most variance and so on.

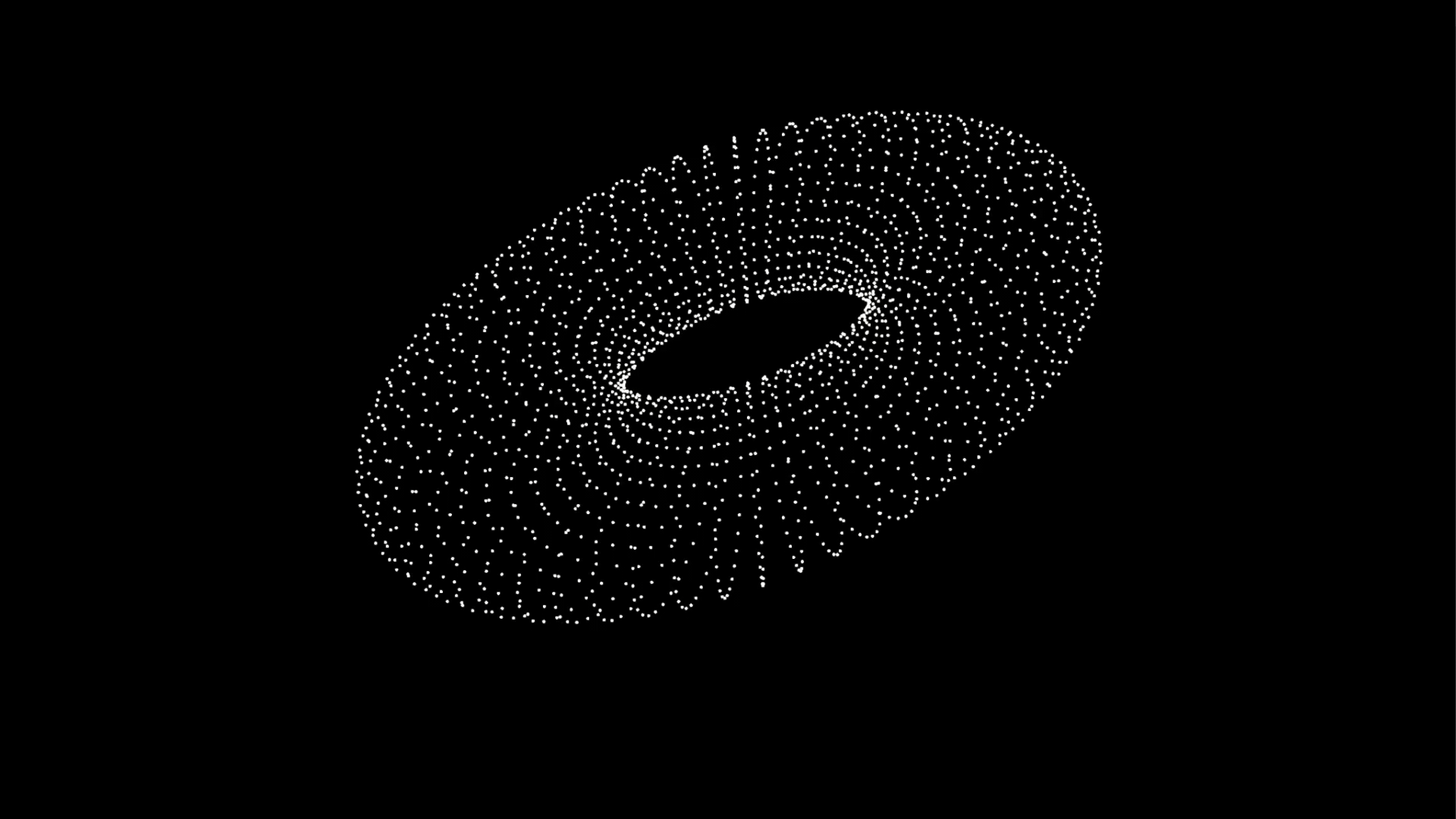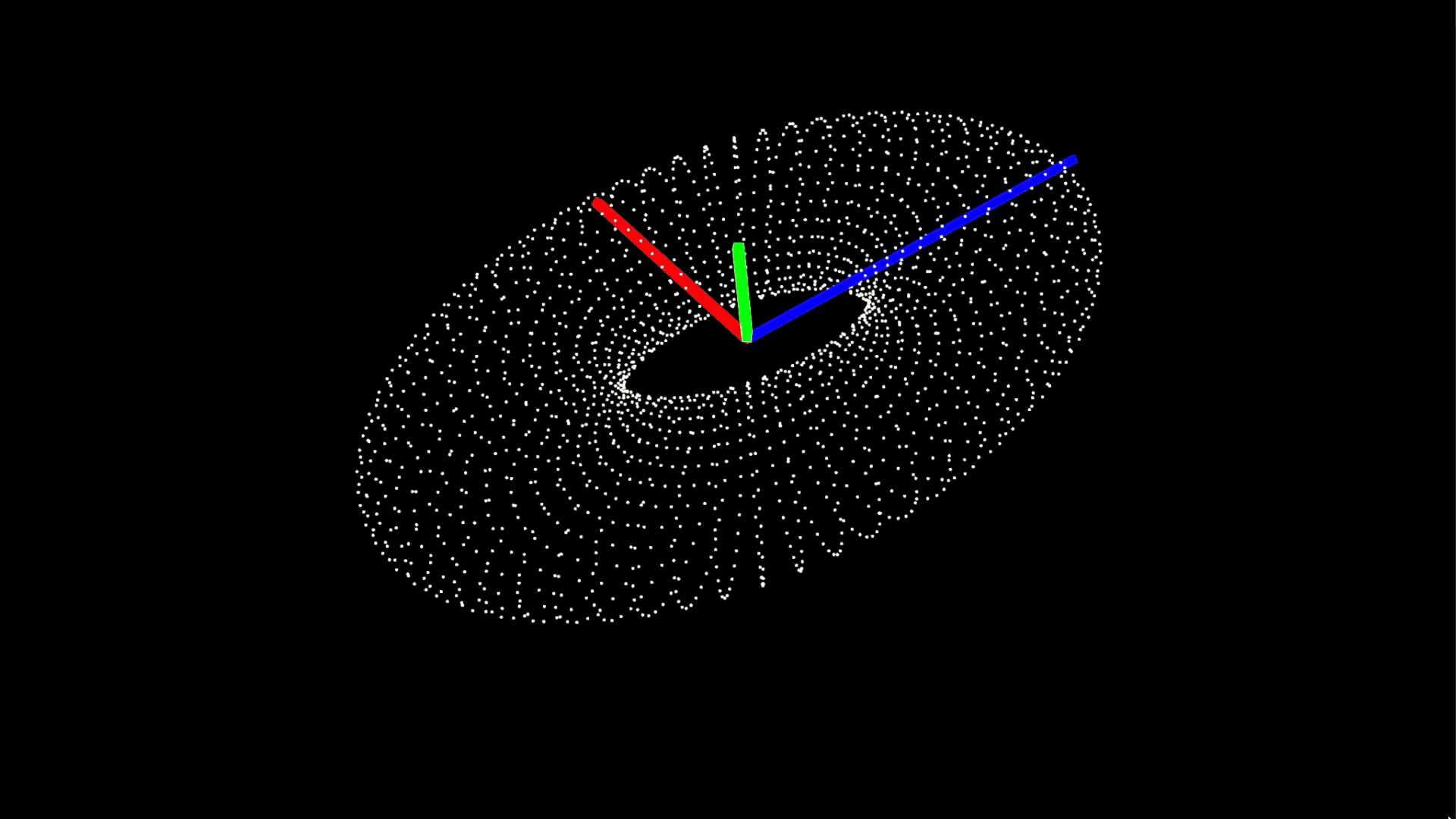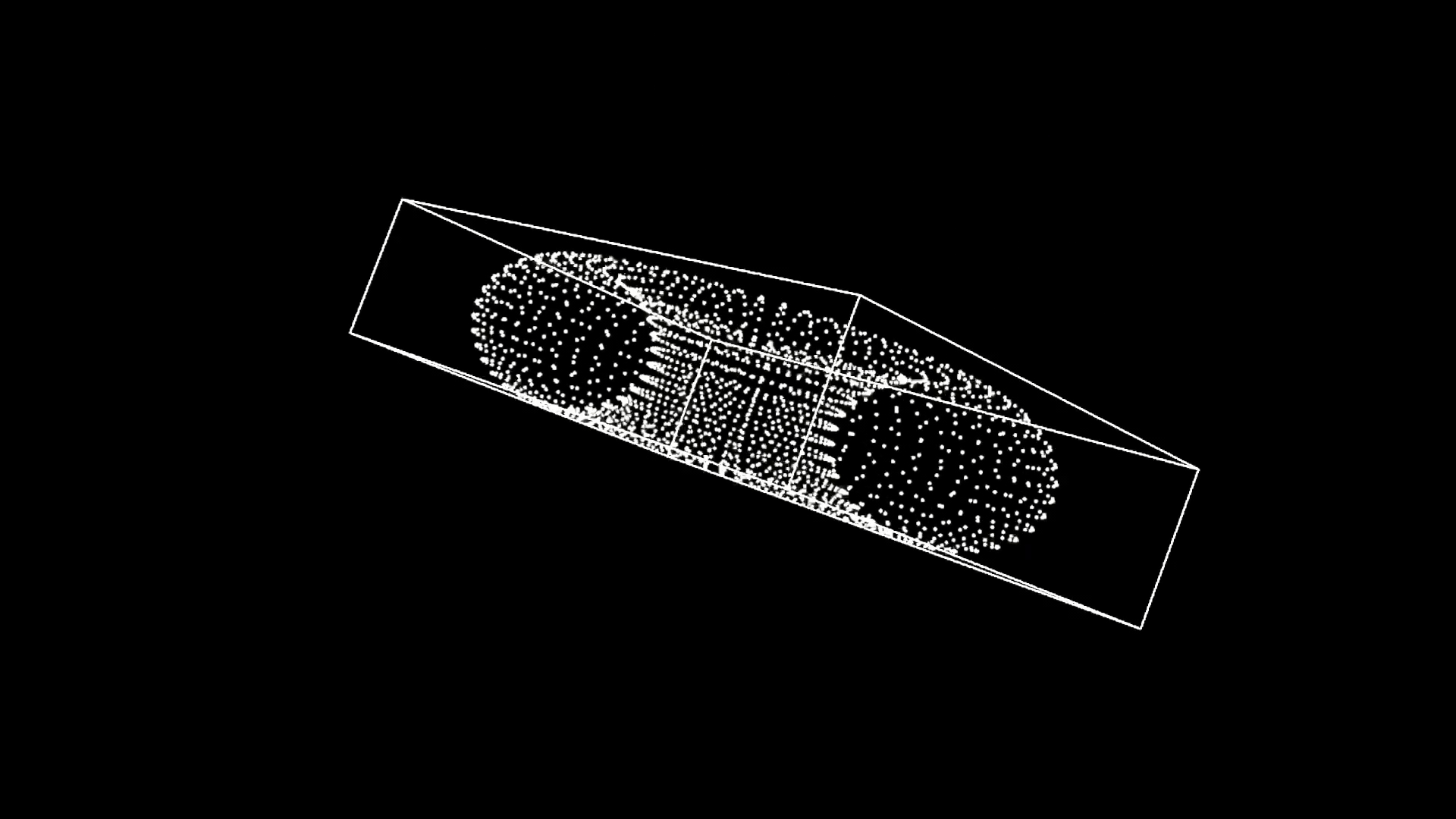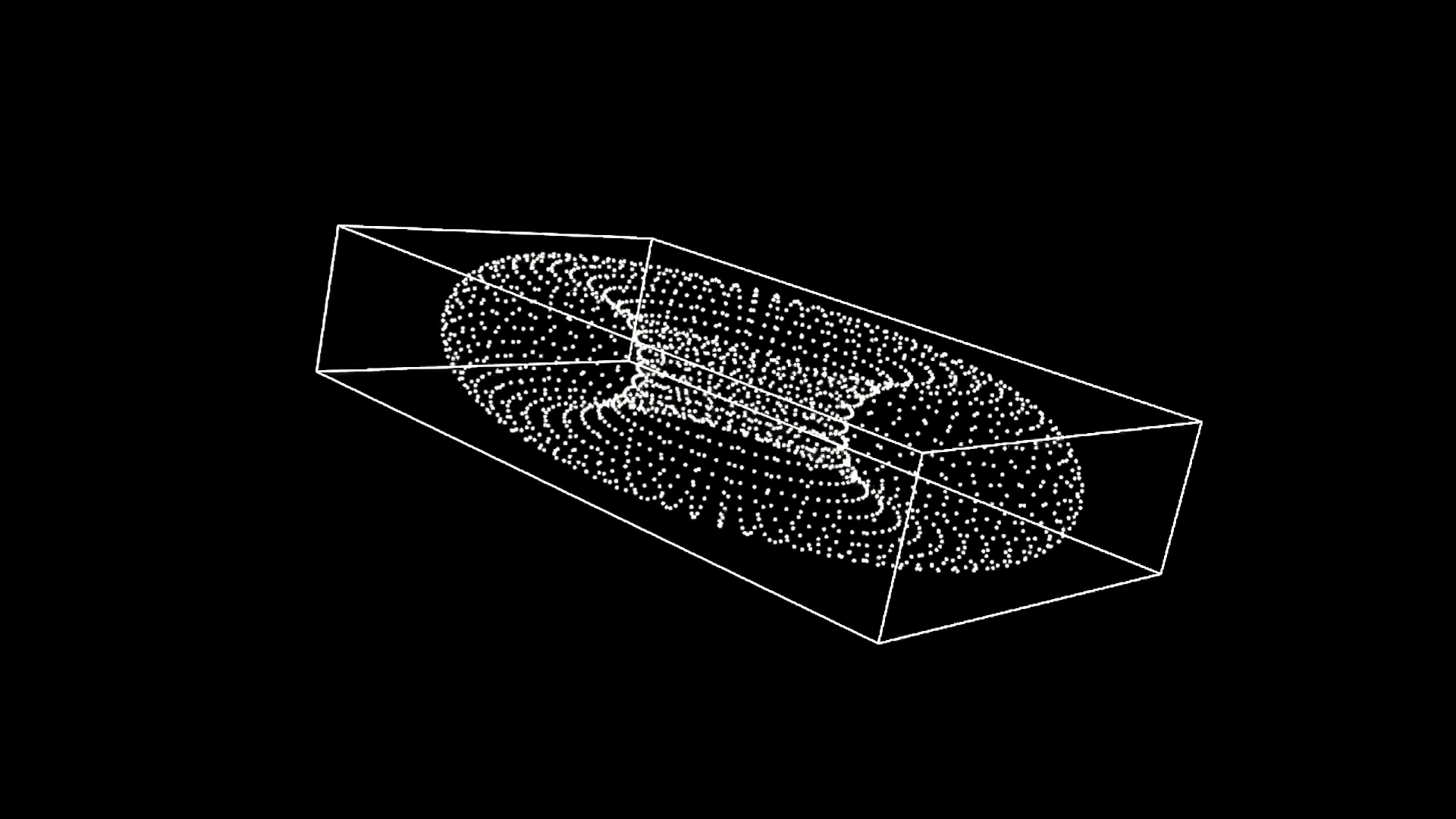
If you visualize those, you get something that already looks like a transform.

The first one (blue) is essentially our Z vector, the second one our X and we can just construct Y using the cross product.

1. The first thing we need to do is center the incoming points on the origin using a matchsize SOP.
2. We stash the transform for later use and call it offset.
3. Then we run PCA on it and compute 3 components (2 are enough but 3 already looks like the axis we will create).
4. Make sure to set points per sample to 1.
5. We can then split point 0 out (this is our origin) and construct the transform matrix on it

// point wrangle “build_matrix”

1
2
3

vector z = normalize(point(1, "P", 0) - v@P); 
vector up = normalize(point(1, "P", 2) - v@P);
4@xform = maketransform(z, up)*invert(4@offset);

6. we can then invert that matrix and lock the point cloud to the world space axis in the origin

// point wrangle “invert_tranform”

1
2
3

4@m = point(1, "xform", 0);
matrix m = invert(4@m);
v@P *= m;

7. In the end we just need to fit a box around it and move everything back to the original position

// point wrangle “transform_back”

1
2

matrix m = point(1, "m", 0);
v@P *= m;

Download: File

An inherent problem with this approach is that the axis flip a lot. The same thing happens in the bound SOP and other implementations. You could counter that by solving the orient forward through time and comparing the orientation to the frame before and flip it back when a big jump in orientation happens.

sources / further reading:

• Oriented Bounding Boxes in VEX - Andy Nicholas
• Principal Component Analysis - Houdini DOCs