Matrix Operations

Last updated Aug 12, 2022 Edit Source

# Basics

# Dimensions

Houdini most commonly uses 3x3 or 4x4 matrices to store transformation data

3x3 -> rotation and scale 4x4 -> rotation, scale and translation

# Identity Matrix

The identity matrix is sort of the base matrix and means no transformation is applied. The diagonal ones store the scale value.

$$ \bigg[\begin{array}{rcl} 1&0&0&0 \\0&1&0&0 \\0&0&1&0 \\0&0&0&1 \\\end{array}\bigg] $$

It can be created in VEX by calling ident().

1
matrix xform = ident();

# Translation

1
2
3
4
5
6
matrix xform = ident();
vector translation = chv("translation");

translate(xform, translation);

@P *= xform;

This is what happens under the hood:

1
2
3
4
5
vector t = chv('translate');

matrix T = set(set(1, 0, 0, 0), set(0, 1, 0, 0), set(0, 0, 1, 0), set(t.x, t.y, t.z, 1));

@P *= T;

# Rotations

Quaternion Rotations

1
2
3
4
5
6
7
matrix xform = ident();
float angle = radians(chf("angle"));
vector axis = chv("axis");

rotate(xform, angle, axis);

@P *= xform;

Euler Rotations

1
2
3
4
5
6
7
8
9
vector rot = radians(chv('rotate'));

matrix3 Rx = set(1,0,0, 0,cos(rot.x),-sin(rot.x), 0,sin(rot.x),cos(rot.x));

matrix3 Ry = set(cos(rot.y),0,sin(rot.y), 0,1,0, -sin(rot.y),0,cos(rot.y));

matrix3 Rz = set(cos(rot.z),-sin(rot.z),0, sin(rot.z),cos(rot.z),0 ,0,0,1);

@P = @P*Rx*Ry*Rz;

for more details have a look at Quaternions and Euler Rotations

# Scale

1
2
3
4
5
6
matrix xform = ident();
vector scale = chv("scale");

scale(xform, scale);

@P *= xform;

# Order of Operations for Transformations

The default of the transform node and in most 3D packages ist SRT, which means first Scaling the object in place and then Rotating it before Translating it’s position.

# Usecases

# Extracting a Transformation Matrix with VEX

Sometimes it’s desirable to lock an animated mesh to the origin to perform further operations. To move it from it’s position in world space to the origin we need it’s transformation matrix.

Paweł Rutkowski has a great video on the topic. The following is basically a writeup of the contents of his video for my own memory and to easily get back to it.

To create a transformation matrix we first have to create a local coordinate system that moves with the object. To do so we have to identify 2 Points that don’t deform and calculate a vector between the two. First isolate the the 2 points by deleting everything else.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
// this goes in point wrangle 1

vector P1 = point(0, "P", 0);
vector P2 = point(0, "P", 1);
vector up = {0,1,0};

vector X = normalize(P2-P1);
vector Z = normalize(cross(X, up));
vector Y = normalize(cross(X, Z));

vector P = P1 + (P2 - P1) / 2;

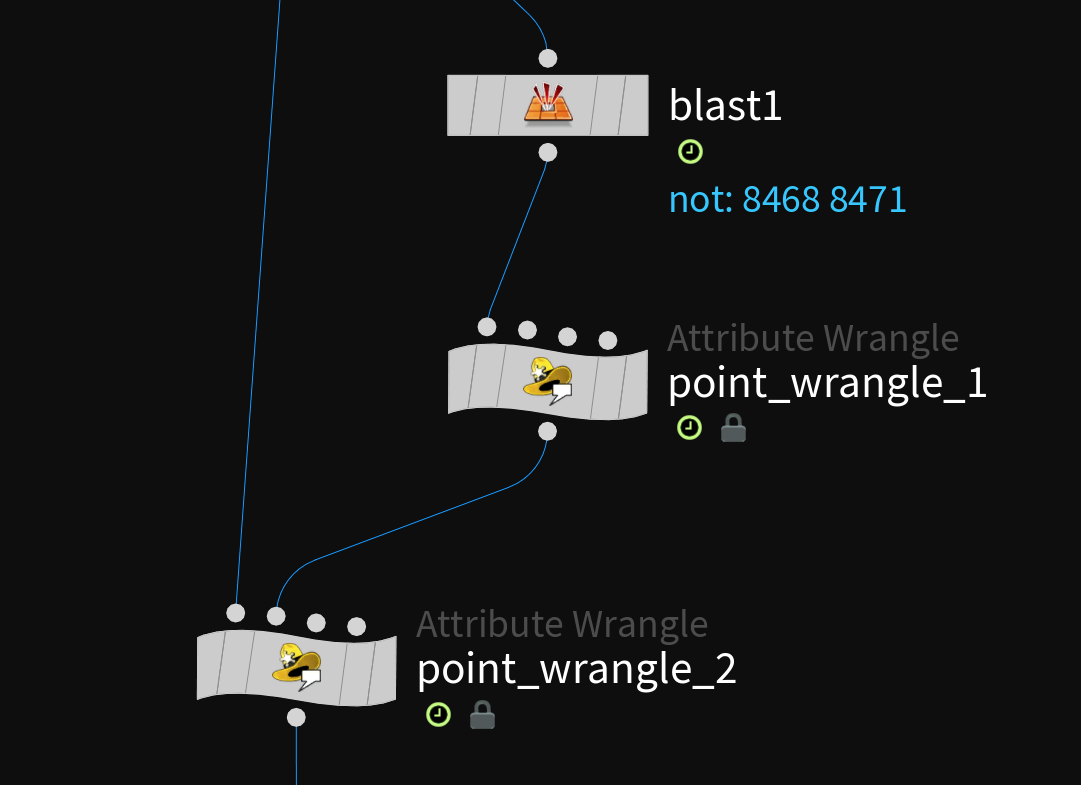
$$ \begin{array}{rcl} \color{red} x-Axis \\\color{green} y-Axis \\\color{blue} z-Axis \\\color{orange} Position \\\end{array} \equiv \bigg[\begin{array}{rcl} \color{red} 1&\color{red}0&\color{red}0&0 \\\color{green}0&\color{green}1&\color{green}0&0 \\\color{blue}0&\color{blue}0&\color{blue}1&0 \\\color{orange}0&\color{orange}0&\color{orange}0&1 \\\end{array}\bigg] $$

We don’t really need the fourth column but 3x4 matrices dont “exist” in VEX.

1
2
3
// this continues the first point wrangle

matrix transform = set(X, Y, Z, P); // create matrix

However this will give us the following matrix with the ones in the fourth column

$$ \bigg[\begin{array}{rcl} \color{red} X.x&\color{red}X.y&\color{red}X.z&1 \\\color{green} Y.x&\color{green}Y.y&\color{green}Y.z&1 \\\color{blue} Z.x&\color{blue}Z.y&\color{blue}Z.z&1 \\\color{orange} P.x&\color{orange}P.y&\color{orange}P.z&1 \\\end{array}\bigg] $$

To fix this we can use the setcomp() function.

1
2
3
4
5
6
7
// this continues the first point wrangle

setcomp(transform, 0, 0, 3); // set row 1 col 4 to 0
setcomp(transform, 0, 1, 3); // set row 2 col 4 to 0
setcomp(transform, 0, 2, 3); // set row 3 col 4 to 0

4@transform = transform; // create matrix attribute

Which will give us the correct transformation matrix:

$$ \bigg[\begin{array}{rcl} \color{red} X.x&\color{red}X.y&\color{red}X.z&0 \\\color{green} Y.x&\color{green}Y.y&\color{green}Y.z&0 \\\color{blue} Z.x&\color{blue}Z.y&\color{blue}Z.z&0 \\\color{orange} P.x&\color{orange}P.y&\color{orange}P.z&1 \\\end{array}\bigg] $$ to move the object to the center the inverted matrix has to be multiplied with the position.

1
2
3
4
5
6
7
// this goes in point wrangle 2

matrix transform = point(1, "transform", 0);

v@P *= invert(transform);
v@N *= matrix3(invert(transform));
v@v *= matrix3(invert(transform));

Download: File

# Warping Space

# Twisting

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
matrix xform = ident();
vector bbox = getbbox_size(0);
vector center = getbbox_center(0);
vector axis = chv("axis");

float min = center.z - bbox.z / 2;
float max = center.z + bbox.z / 2;

float rotations = chf("rotations");

float angle = fit(@P.z, min, max, -PI*rotations, PI*rotations);

rotate(xform, angle, axis);

@P *= xform;

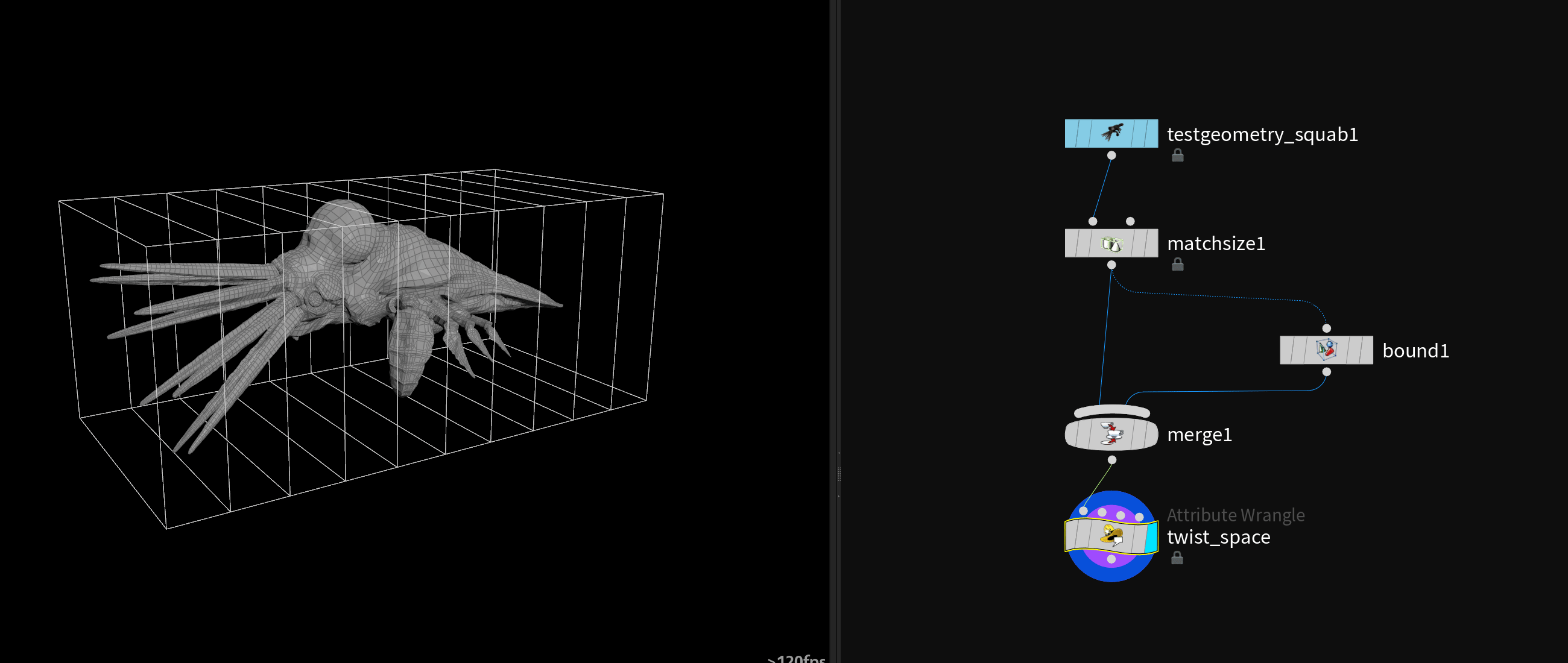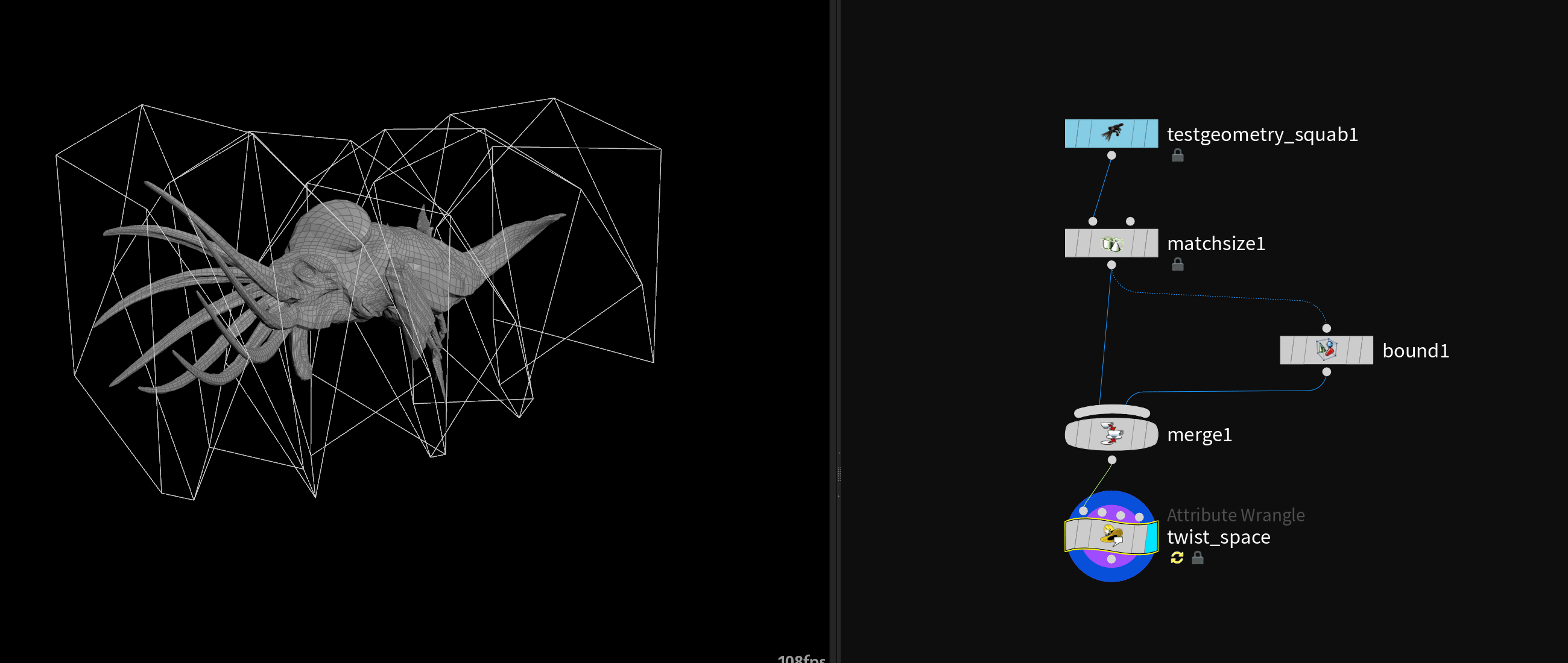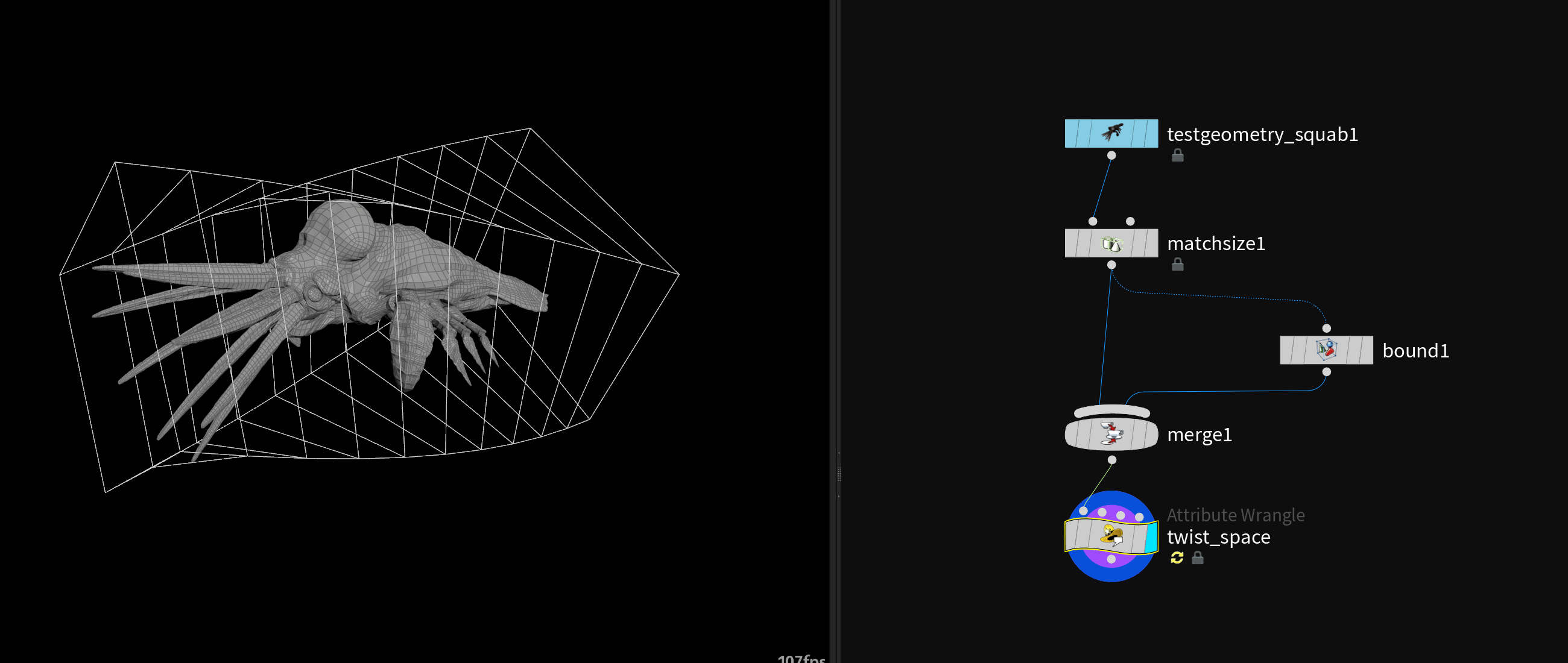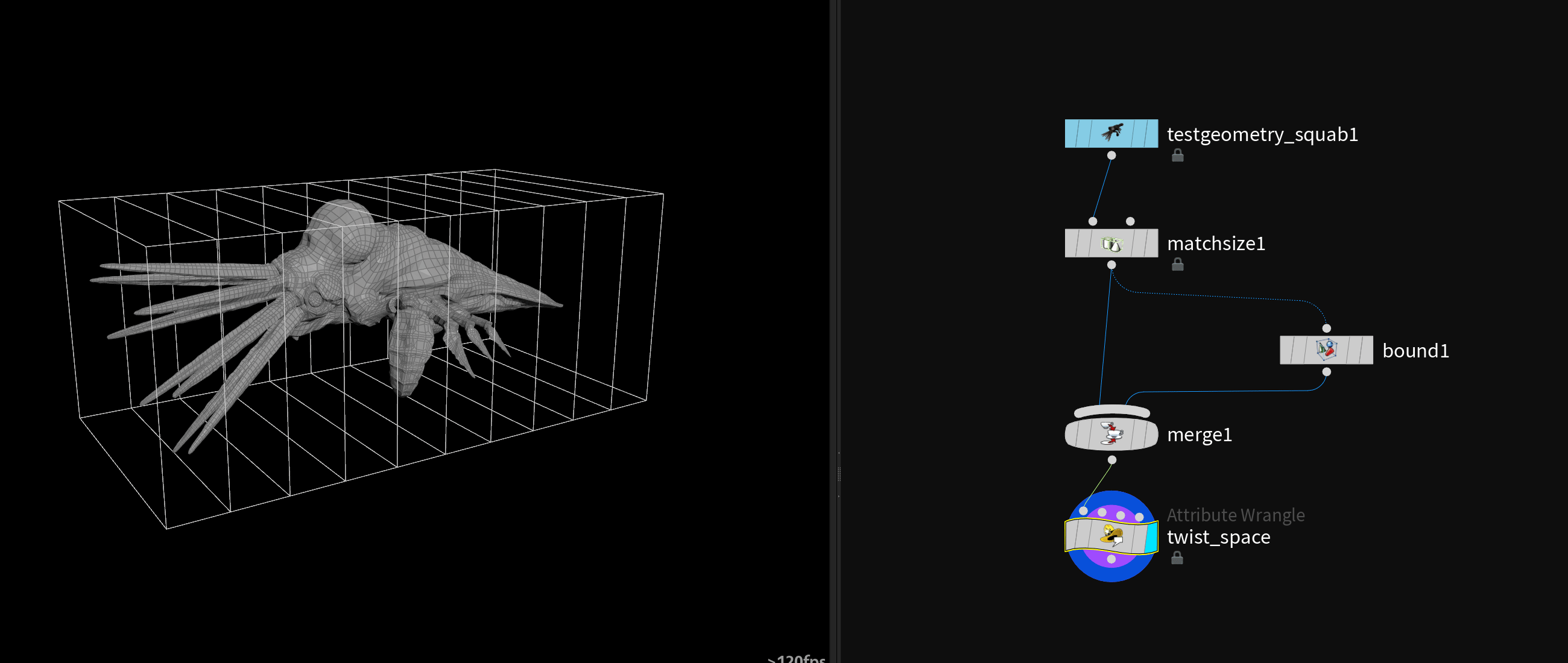
# Black Hole Vortex

John Kunz demonstrated this technique in his Pure VEX Workshop Week 6.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
matrix xform = ident();

vector angle = (1.0 / exp(length(@P)))*chv("rotationscale");
float scale = pow(1 - 1 / exp(length(@P)), 5);
vector translatedir = chv("translatedir")*chf("translatescale");
vector translate = set(translatedir.x, translatedir.y, translatedir.z) / exp(length(@P));

rotate(xform, angle.x, set(1,0,0) );
rotate(xform, angle.y, set(0,1,0) );
rotate(xform, angle.z, set(0,0,1) );

scale(xform, scale);

translate(xform, translate);

@P *= xform;

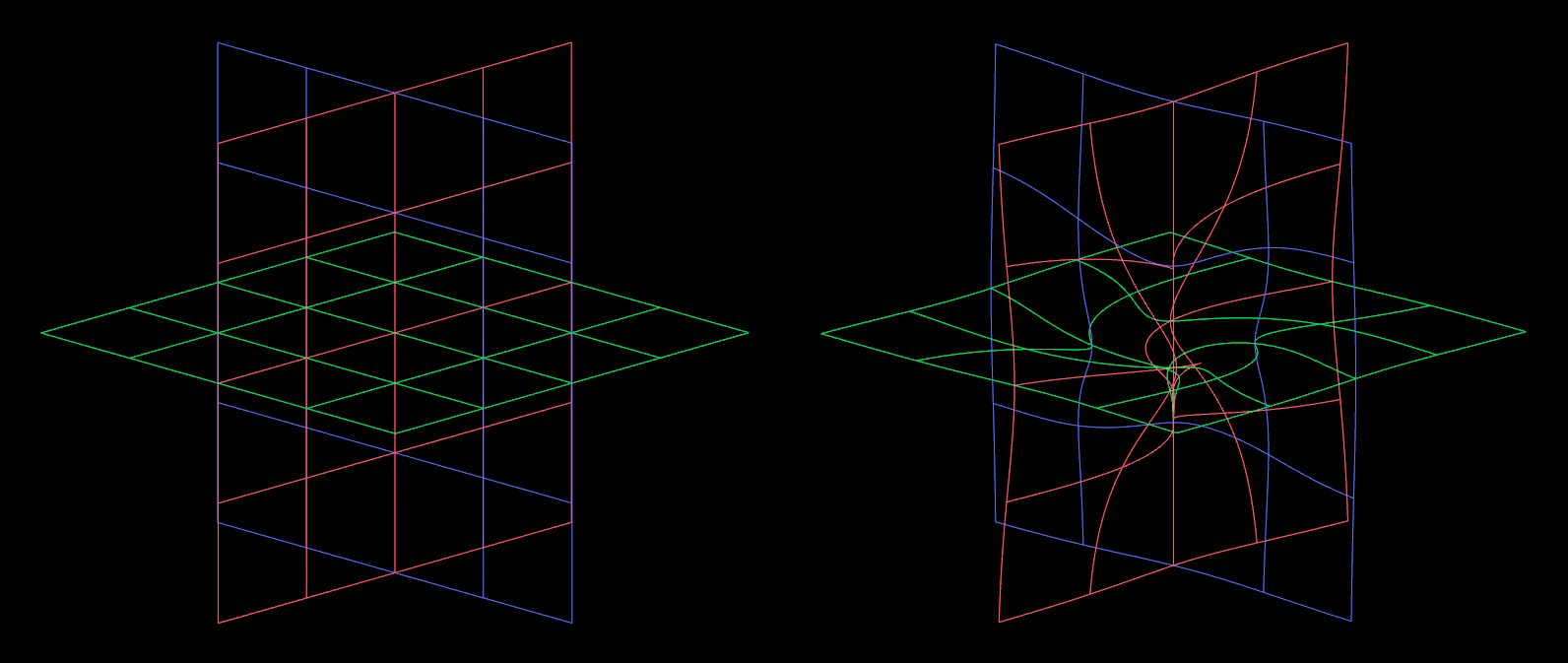
sources / further reading

fx notes