Quaternion & Euler Rotations

Last updated Oct 24, 2023 Edit Source

• Houdini
• Math
• Vex

expressed as 4 numbers vector4 = [x, y, z, w]

It’s usually used to define rotational transformation in 3D Space. To do so it needs 2 types of information:

• rotational angle $\theta$
• rotational axis $A$

The 4 vector values of a quaternion are calculated in the following way:

$q = (sin(\frac{\theta}{2})*Ax, sin(\frac{\theta}{2})*Ay, sin(\frac{\theta}{2})*Az, cos(\frac{\theta}{2}))$

In VEX we can use the quaternion function which accepts an angle in radians and an axis vector to propagate the vector4 accordingly.

1
2
3
4
5
6
7

//this goes in a point wrangle

float angle = chf("angle");
vector axis = normalize(chv("axis"));

vector4 rot = quaternion(radians(angle), axis);
@P = qrotate(rot, @P);

While Quaternians define the rotational transformation with an angle around a specified axis, Euler rotation is defined by 3 Parameters (compare Transform Node x, y, z).

To convert Euler rotations to quaternions we need to specify the rotation order:

1
2
3
4
5
6
7
8

vector angles = chv("angles");
angles = radians(angles);

int order = XFORM_XYZ; // integer arguments are defined in $HH/vex/include/math.h

vector4 rot = eulertoquaternion(angles, order);

p@quat = rot;

Rotation Order Integer Arguments as defined in $HH/vex/include/math.h:

1
2
3
4
5
6

#define XFORM_XYZ 0 // Rotate order X, Y, Z
#define XFORM_XZY 1 // Rotate order X, Z, Y
#define XFORM_YXZ 2 // Rotate order Y, X, Z
#define XFORM_YZX 3 // Rotate order Y, Z, X
#define XFORM_ZXY 4 // Rotate order Z, X, Y
#define XFORM_ZYX 5 // Rotate order Z, Y, X

Same thing works backwards:

1
2
3
4
5

vector4 quat = p@quat;

vector euler = quaterniontoeuler(quat, XFORM_XYZ);

v@euler = degrees(euler);

Matrices can do most of what quaternions can do and more (translation & scale). However, one thing that quaternions enable you to do is using the slerp function to blend smoothly between two rotational transformations.

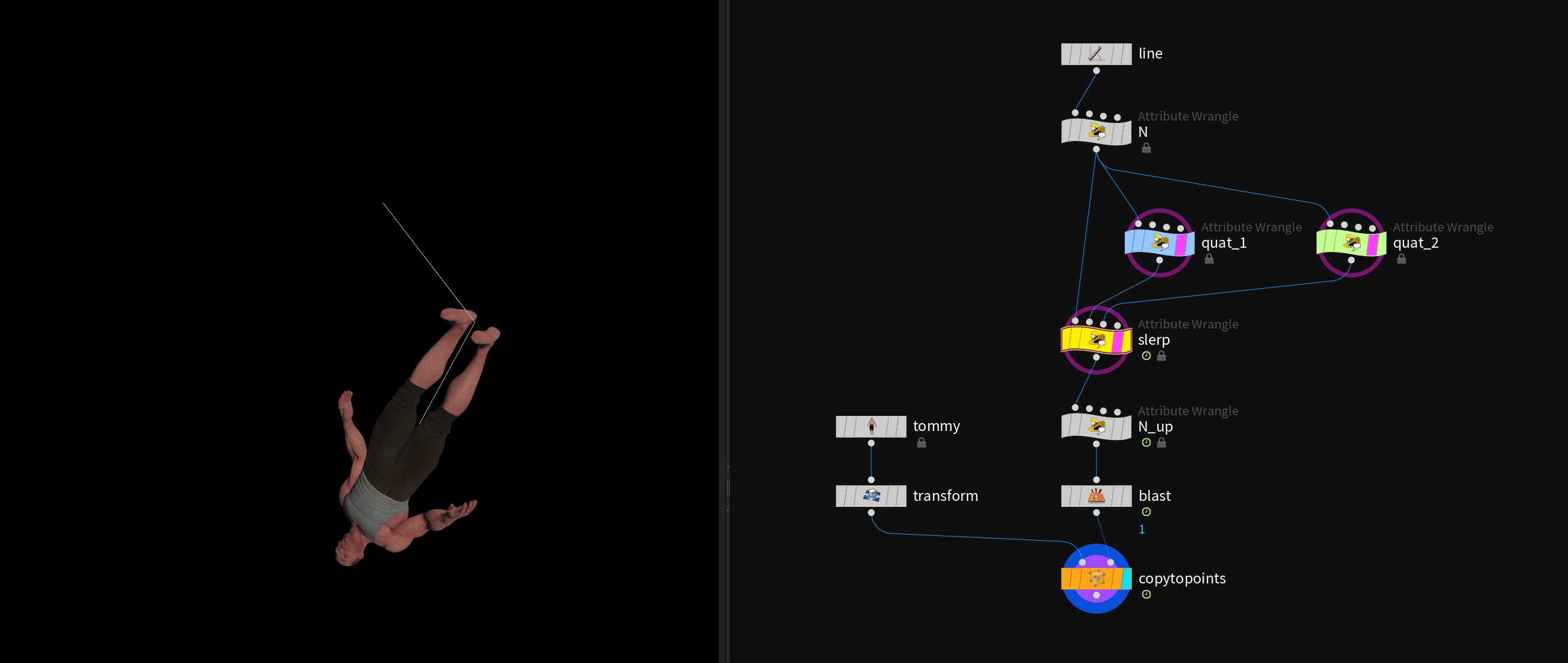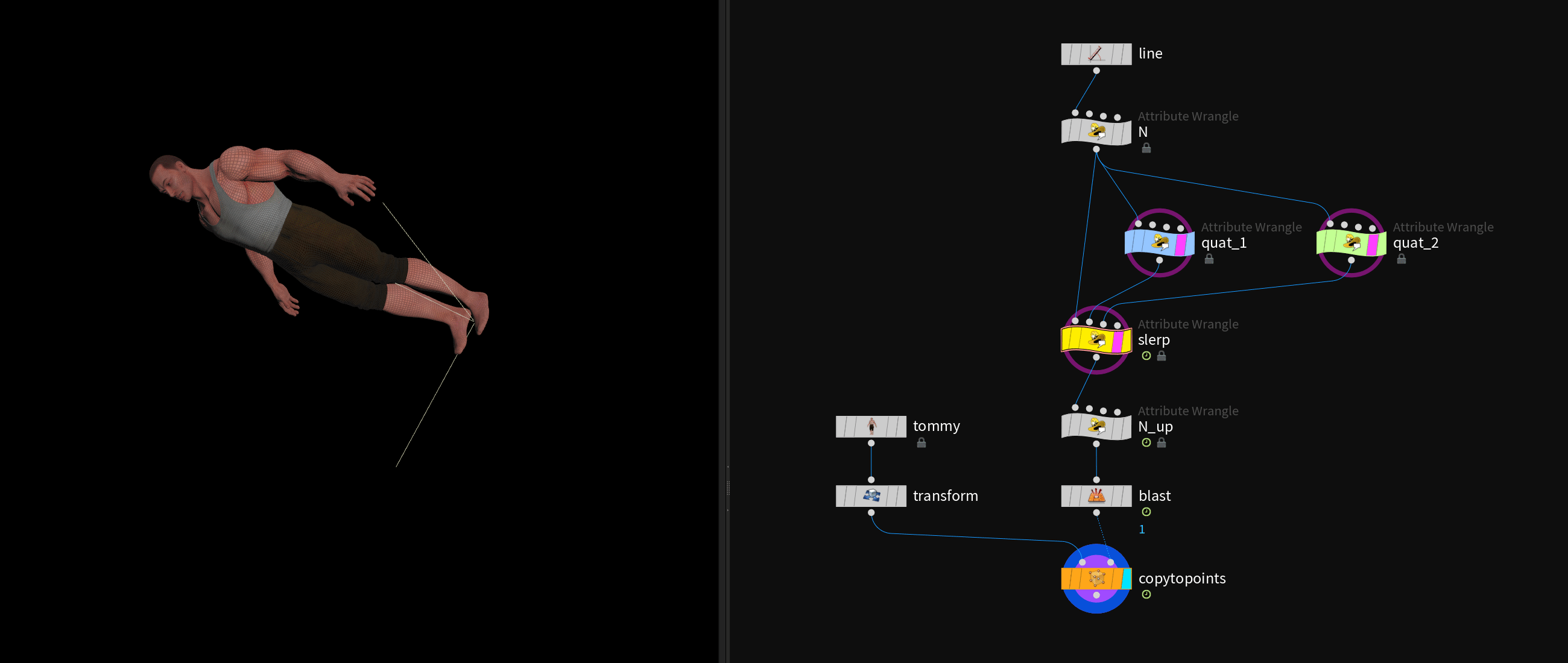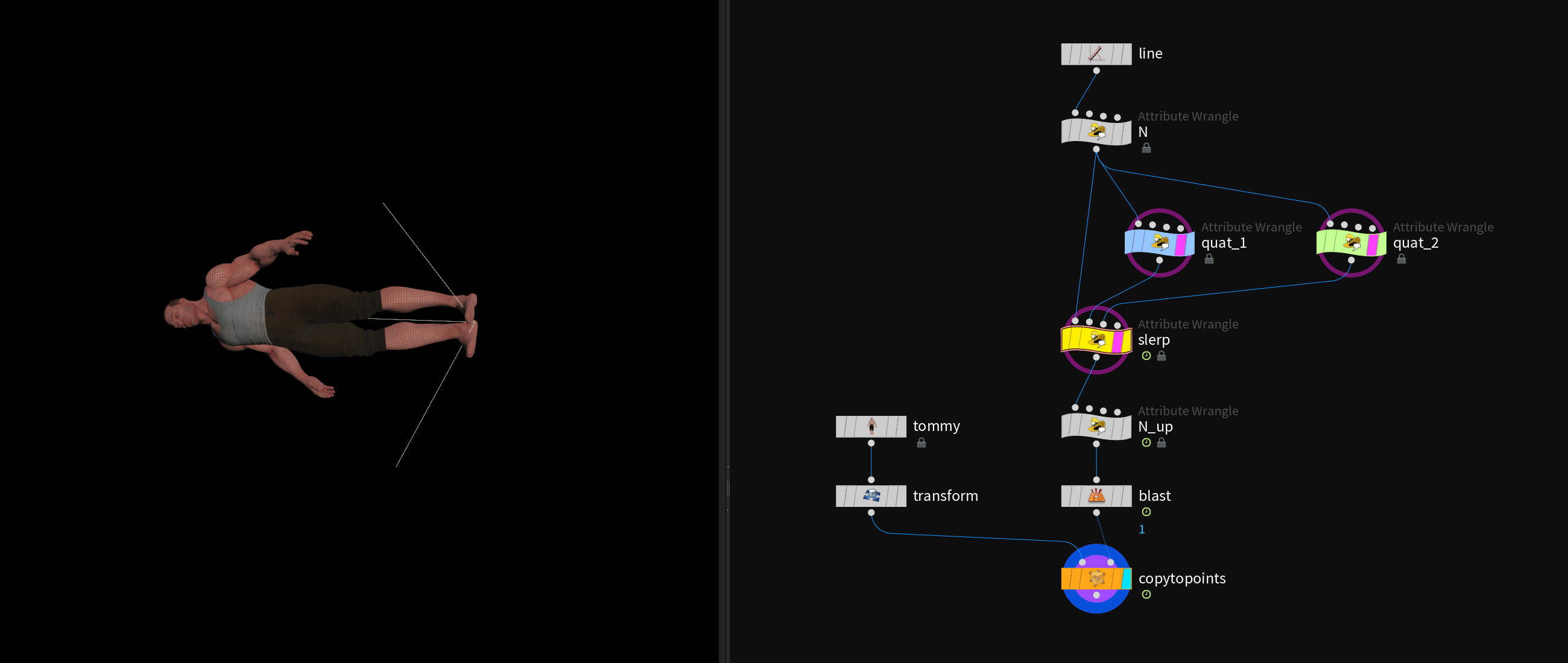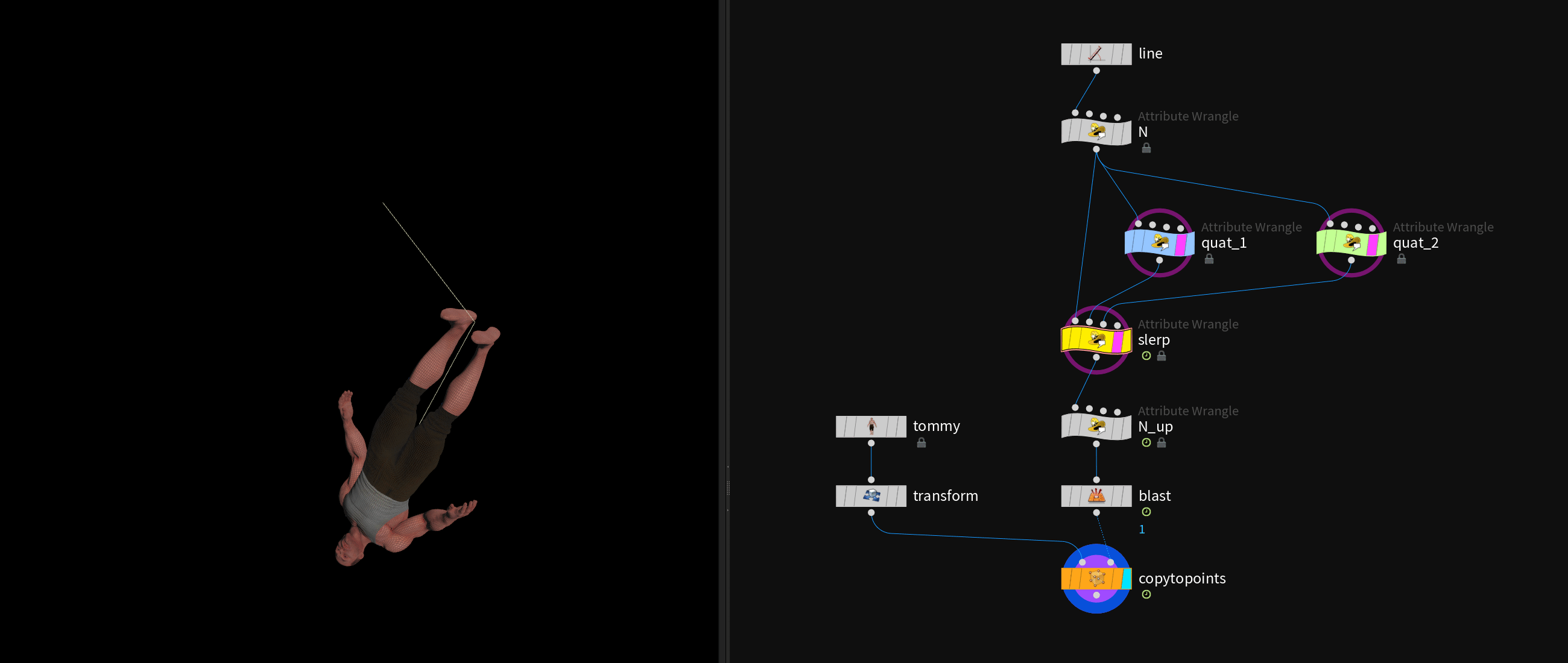
In this example the two orientations get initialized buy rotating a line in two different ways and extracting each quaternion.

1
2
3
4
5
6
7
8
9

// this goes in point wrangle "quat_1 & 2"

float angle = chf("angle");
vector axis = normalize(chv("axis"));

vector4 rot = quaternion(radians(angle), axis);
@P = qrotate(rot, @P);

p@quat = rot;

Then we can blend rotationally between the two orientations with the slerp function and apply the blended result.

1
2
3
4
5
6
7
8
9

// this goes in point wrangle  "slerp"

vector4 quat1 = point(1, "quat", 1);
vector4 quat2 = point(2, "quat", 1);

vector4 rot = slerp(quat1, quat2, chf("blend"));

@P = qrotate(rot, @P);
@N = qrotate(rot, @N);

Download: File

The dihedral function creates a quaternion that describes the rotational transformation between two given vectors. This can be used to switch between two orientations of a mesh.

1
2
3
4
5
6

vector v1 = normalize(point(1, "P", 1));
vector v2 = normalize(point(2, "P", 1));

vector4 quat = dihedral(v1, v2);

@P = qrotate(quat, @P);

• [VEX for Algorithmic Design] E14 _ Quaternion Basics - Junichiro Horikawa
• Visualizing quaternions - Grant Sanderson (3blue1brown)

• Matrix Operations