Strange Attractors

Last updated Oct 31, 2024 Edit Source

• Houdini
• Math

Strange attractors are patterns that emerge in chaotic systems. Even though the individual movements can seem random and unpredictable, strange attractors show a kind of underlying order. They represent points in the system’s phase space where trajectories tend to cluster over time, creating intricate and often beautiful shapes.

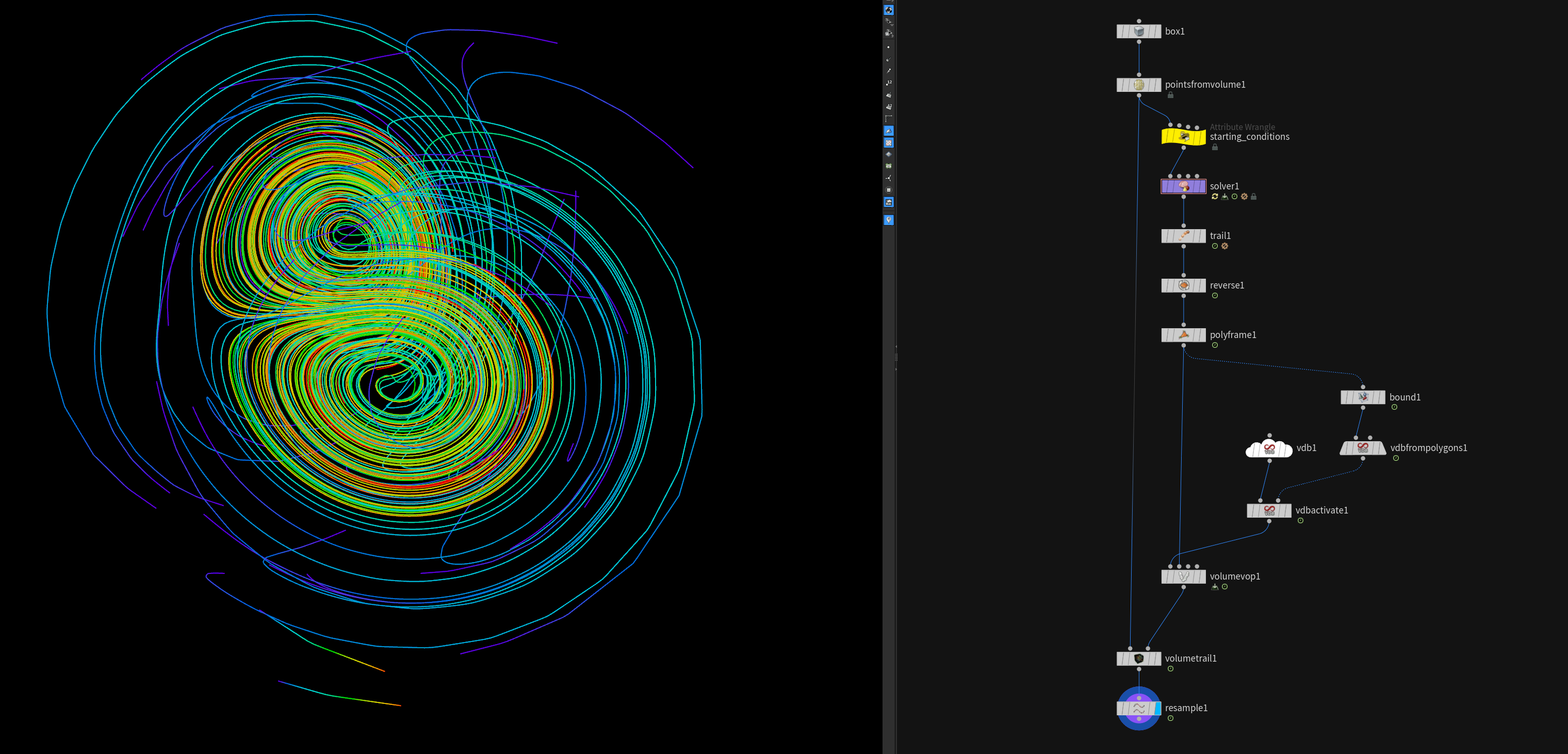
//pointwrangle “starting_conditions” (used the values in each comment)

1
2
3
4

@a = chf("sigma"); // 10
@b = chf("rho");   // 28
@c = chf("beta");  // 8/3
@dt = ch("dt");    // 0.002

The solver is just a point wrangle that moves the starting points along based on the formula and starting conditions.

// the solver

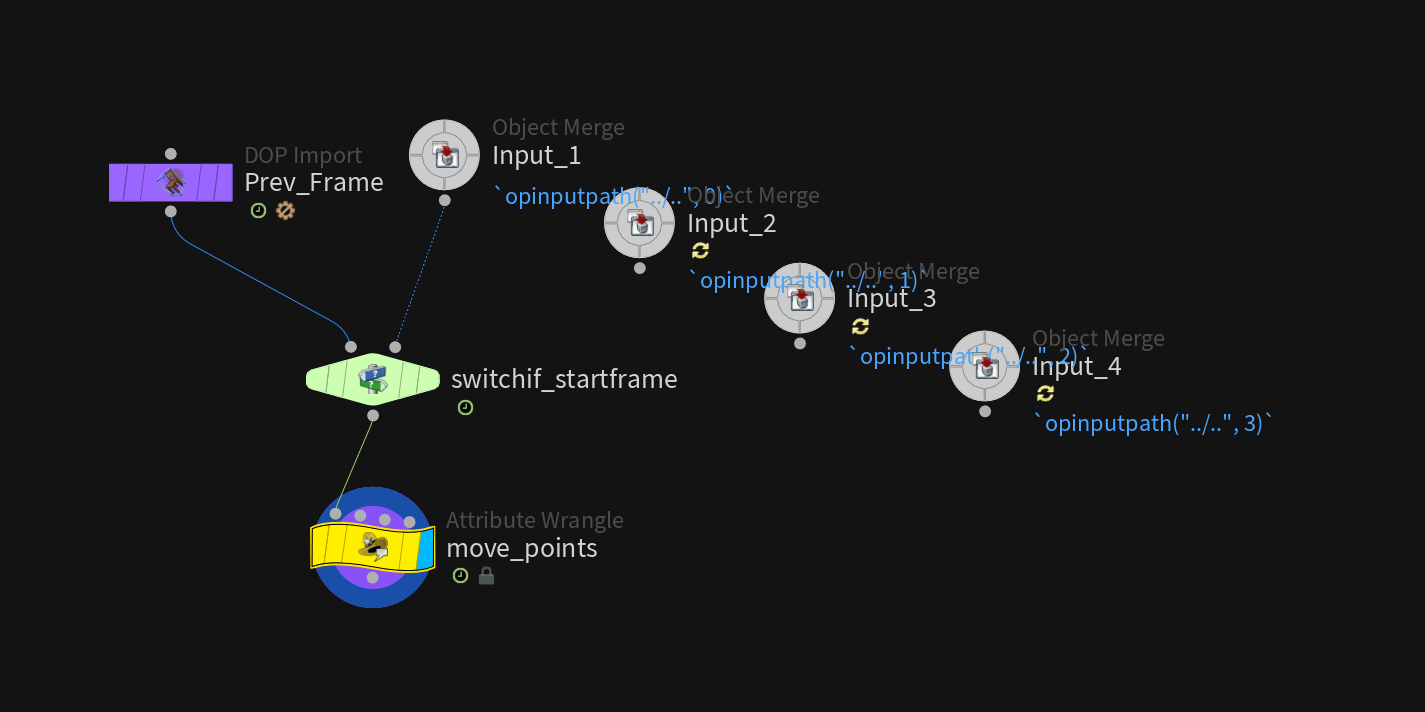
//pointwrangle “move_points”

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

float x = @P.x;
float y = @P.y;
float z = @P.z;

float dx = (@a * ( y - x )) * @dt;
float dy = (x * ( @b - z ) - y ) * @dt;
float dz = (x * y - @c * z ) * @dt;

@P.x += dx;
@P.y += dy;
@P.z += dz;

sources / further reading:

• Darstellung von Attraktoren mit Cinema - 3d Meier
• Houdini Tutorial 0034 Strange Attractor (Slow version) - Junichiro Horikawa
• VEX in Houdini: Strange Attractors - Entagma
• Coding Challenge #12: The Lorenz Attractor in Processing - The Coding Train
• Chaos: The Science of the Butterfly Effect - Veritasium